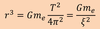chapter 2: Orbits and Navigation

Question 1

The gravitational and astronomical laws were originally formulated to explain

Answer 1

the motion of planets in the solar system and their orbits around the sun.

Question 2

…………………………were originally formulated to explain
the motion of planets in the solar system and their orbits around the sun.

Answer 2

The gravitational and astronomical laws

Question 3

These laws (Newtonian and Keplerian) are equally applicable to

Answer 3

the orbits of artificial satellites placed around the earth.

Question 4

…………………….the orbits of artificial satellites placed around the earth.

Answer 4

These laws (Newtonian and Keplerian) are equally applicable to

Question 5

Newton’s Law of Universal Gravitation

Answer 5

The force of attraction between two point masses m1 and m2 separated by a distance r is

Question 6

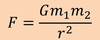
where G is

Answer 6

is theUniversal gravitation constant(6.67259x10‐11 N m2 kg‐2).

Question 7

the following is

Answer 7

Newton’s Law of Universal Gravitation

The force of attraction between two point masses m1 and m2 separated by a distanceris:

Question 8

Consider the simple circular orbit shown in Figure. Assuming that the Earth is a ……………………, we can treat it as ………………….

Answer 8

sphere, we can treat it as a point mass

Question 9

The centripetal force is required to

Answer 9

keep the satellite in a circular orbit is rnv^2/r, here v is the orbital velocity of the satellite.

Question 10

………………………………….. that balances this centripital force is ……………………..

Answer 10

The force of gravity (F)

Gm_em/r²

Question 11

Theforce of gravity (F) that balances thiscentripetal forceis Gm_em/r²
,where m_e is

and m is

Answer 11

the mass of the Earth (5.97370x10²⁴kg)

the mass of the satellite

Question 12

Theforce of gravity (F) that balances thiscentripetal forceis Gmem/r2
,whereme is the mass of the Earth (5.97370x10²⁴kg) and mis the mass of the
satellite. Equating the two forces gives:

Answer 12

Question 13

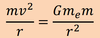
Division bym eliminates the mass of the satellite from the equation, which
means that

Answer 13

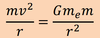
the orbit of a satellite is independent of its mass

Question 14

Orbital Period (T):

Answer 14

The time taken by a satellite to travel around its orbit once is known as the
period.

Question 15

The period of an orbit simply depends on

Answer 15

its altitude

Question 16

The period of the satellite is

Answer 16

the orbit circumference divided by the velocity:
T=2πr/v

Question 17

orbital period =

Answer 17

Question 18

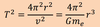
For any given height above the Earth’s surface, a satellite will

Answer 18

take a fixed time
to complete an orbit, regardless of the mass of the satellite.

Question 19

for …………………………………………… a satellite will take a fixed time to complete an orbit, regardless of the mass of the satellite.

Answer 19

For any given height above the Earth’s surface

Question 20

Kepler’s laws of motion:

Answer 20

1. law of orbits
2. law of areas
3. law of periods

Question 21

Kepler’s laws of motion state that:

1.

Answer 21

Law of orbits: All planets travel in elliptical paths with the sun at one focus.

Question 22

Kepler’s laws of motion state that:

2.

Answer 22

Law of areas: The radius vector from the sun to a planet sweeps out equal areas in equal times

• This empirical law discovered by Kepler arises from conservation of angular momentum.
• When the planet is closer to the sun,it moves faster, sweeping through a longer path in a given time.

Question 23

Kepler’s laws of motion state that:

3.

Answer 23

Law of Periods: The ratio of the square of the period of revolution of a planet to the cube of its semimajor axis (radius of orbit) is the same for all planets revolving around the sun.

Question 24

Kepler’s laws of motion

These laws are also applicable to

Answer 24

the artificial satellites placed in elliptical orbits (also called Keplerian orbits) around the earth at one focus.

Question 25

define perigee

Answer 25

The point where the satellite most closely approaches the Earth

Question 26

perigee more generally the

Answer 26

perifocus

Question 27

apogee is also known as

Answer 27

apofocus

Question 28

apogee or apofocus:

Answer 28

The point where the satellite is furthest from the Earth

Question 29

semimajor axis is denoted by the symbol

Answer 29

a

Question 30

semimajor axis:

Answer 30

The distance from the center of the ellipse to the perigee (or apogee)

Question 31

the eccentricity (E):

Answer 31

The distance (a_E) from the center of the ellipse to one focus (to the center of the Earth) divided by the semimajor axis (a)

Question 32

For an ellipse, the eccentricity is a number between

Answer 32

0 and 1 (0 < E < 1)

Question 33

A circle is an ellipse with

Answer 33

zero eccentricity

Question 34

The equation for the elliptical path that the satellite follows, in polar coordinates with the Earth as origin is given as:

Answer 34

Question 35

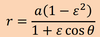
the angle O- is

Answer 35

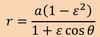
the true anomaly and is always measured counter clockwise (the
direction of satellite motion) from the perigee.

Question 36

The two basic types of meteorological satellite orbits are:

Answer 36

1. Geostationary orbit – high altitude orbit over the equator
2. Polar orbit – low altitude orbit from pole to pole

Question 37

Geostationary orbit:

Answer 37

• A satellite in this orbit will remain stationary relative to the earth’s surface.
• For any orbit to be geostationary, it must be geosynchronous and circular with zero inclination over the equator.

Question 38

A geosynchronous orbit is

Answer 38

any orbit with an orbital period equal to the earth’s rotational period.

Question 39

A geosynchronous satellite completes one orbit around the earth in the same
time

Answer 39

that the earth takes to make one rotation

Question 40

A geosynchronous satellite completes one orbit around the earth in the same time that the earth takes to make one rotation

This time period is known as …………………………. and is equivalent to ………………………….

Answer 40

onesidereal day and is equivalent to 23 h 56 m 04 s

Question 41

This time period is known as onesidereal dayand is equivalent to 23 h 56 m 04 s .It represents the

Answer 41

time taken by the earth to rotate on its axis relative to the stars, and is almost four minutes shorter than the solar day.

Question 42

To achieve this earth’sorbital period,the satellite should have

Answer 42

the same angular velocity as the earth.

Question 43

To achieve this earth’sorbital period,the satellite should have the sameangular
velocityas the earth. Based on the Kepler’s laws, to achieve this, the satellite
must be placed at a height of

Answer 43

35,786 km above the earth

Question 44

To achieve this earth’sorbital period,the satellite should have the sameangular
velocityas the earth. Based on the Kepler’s laws, to achieve this, the satellite
must be placed at a height of 35,786 km above the earth.

That is, to achieve the earth’s angular velocity of ……………………………………. the satellite altitude can be calculated from

Answer 44

ς = 7.292 x 10^-5 s^-1

Question 45

To ensure that a satellite remains over a particular point on the earth’s surface, the orbit must also be

Answer 45

circular and havezero inclination over the equator.

Question 46

However, a geosynchronous orbit has an inclination of

Answer 46

20 degrees

Question 47

However, a geosynchronous orbit has an inclination of 20 degrees, because of
which a geosynchronous satellite will move

Answer 47

north and south of the equator during its orbit while the geostationary satellite will not.

Question 48

Therefore, geostationary satellites are those which orbit with a period

Answer 48

equal to the earth’s rotational period and with zero eccentricity and zero inclination

Question 49

The theoretical coverage area of a geostationary satellite extends to about

Answer 49

40% of the Earth’s surface.

Question 50

………………………………..can provide full coverage of the Earth, except for ………………………….

Answer 50

A constellation of three equally spaced geostationary satellites

the polar regions

Question 51

As satellites in geostationary orbit continuously cover a large portion of the
Earth, this makes it an ideal orbit for

Answer 51

telecommunications or for monitoring continent‐wide weather patterns and environmental conditions

Question 52

As satellites in geostationary orbit continuously cover a large portion of the
Earth, this makes it an ideal orbit for telecommunications or for monitoring
continent‐wide weather patterns and environmental conditions.
It also ………….. cost as ……………………………………………………………

Answer 52

decreases

as ground stations do not need to track the satellite.

Question 53

Major disadvantage of this high altitude satellite is, of course,

Answer 53

a low resolution in the images (the typical resolution can be 1 to 4 km).

Question 54

Some of the operational geostationary satellites are:

Answer 54

GOES (US), METEOSAT (Europe) and INSAT (India)

Question 55

Polar orbit

Answer 55

The main objective of the satellites rotating in these low‐altitude, high inclination polar‐orbits is ‘global coverage’ with high spatial resolution.

Question 56

The polar orbiting satellites fly in ………….orbits

Answer 56

much lower orbits typically at around 850 km

Question 57

The polar orbiting satellites fly in much lower orbits typically at around 850 km, with the orbital plane at

Answer 57

an angle of about 80^o to the equator.

Question 58

the period of these satellites is given by:

Answer 58

Question 59

Thus, these satellites circle the earth from

Answer 59

pole to pole once in less than 2 hours (T = 104 min) i.e., they circle the earth 14 times each day.

Question 60

As the earth rotates to the …………….. beneath the satellite, each pass ………………………………………to the ………… of the previous pass

Answer 60

east

monitors an area to the west of the previous pass.

Question 61

Each polar‐orbiting satellite can typically observe

Answer 61

the entire planet twice in 24‐ hours, once during daylight and once at night

Question 62

Each polar‐orbiting satellite can typically observe the entire planet twice in 24‐
hours, once during daylight and once at night, with …………………. resolution than the ………………………………….

Answer 62

better resolution than the geostationary satellites.

Question 63

The orbital plane of these satellites is…………………………, which means ……………………………………….. . hence, this orbit is also known as

Answer 63

fixed relative to the Sun

that the plane of the orbit keeps a constant angle with the sun throughout the year.

sun‐synchronousorbit

Question 64

The sun‐synchronous orbit ensures that the satellite

Answer 64

passes over a given location on the earth at the same local time each day.

Question 65

Some of the operational polar orbit satellites are:

Answer 65

TIROS‐N / NOAA‐A (US), METEOR‐2 (Russia), SPOT (France), ERS‐1 (Europe)

Question 66

Comparison of the characteristics of Geostationary and Polar‐orbiting satellites

Answer 66

Question 67

To define the position of a point on the celestial sphere (……………………..) we use the …………………………….. known as

Answer 67

an imaginary sphere of infinite radius surrounding the earth

celestial equatorial coordinate system

known as the Right Ascension‐Declination Coordinate System.

Question 68

Like terrestrial coordinates (i.e., latitude and longitude), the two coordinates to define a point on the celestial sphere are:

Answer 68

the declination and the right ascension.

Question 69

declination

Answer 69

The coordinate indicating where an object is between the celestial poles

Question 70

Declinationis measured

Answer 70

from the celestial equator

Question 71

……………………is measured from the celestial equator

Answer 71

declination

Question 72

Declinationis measured from the celestial equator

it extends from

Answer 72

0° at the celestial equator to +90° at the north celestial pole and from 0° at celestial equator to‐90° at the south celestial pole.

Question 73

right ascension

Answer 73

the second coordinate in the celestial equatorial system

• It is analogous to longitude of the terrestrial coordinates.
• Like Greenwich which is the arbitrary zero point for longitude, right ascension also has a zero reference point atVernal Equinox.
• Right ascension, consequently, is measured in (sidereal) hours, 0h to 24h east from the Vernal Equinox Point. That is, east is the direction of increasing right ascension.

Question 74

equinoxes

Answer 74

The intersections of theecliptic(apparent path of the satellite) with the celestial equator

Question 75

Consequently, the vernal equinox point:

the autumnal equinox point:

Answer 75

Consequently, the vernal equinox point (RA = 00h 00m 00s) and the autumnal equinox point (RA = 12h 00m 00s).

Question 76

The position of the satellite at any given time can be correctly identified, if

Answer 76

a set of parameters (orbital elements) fully describe a satellite orbit, are known.

Question 77

The sixorbital elements, which completely determine the motion of a satellite are:

Answer 77

Question 78

The semimajor axis and eccentricity define the

Answer 78

size and shape of the ellipse

Question 79

right ascension of ascending node, inclination angle andargument of perigee combine to

Answer 79

position the ellipse relative to the Earth.

Question 80

These five parameters define the

Answer 80

shape and location of the orbital path

Question 81

mean anomaly:

Answer 81

“how far round” the ellipse the satellite lies at any given time

Question 82

Thus the first two parameters give the

Answer 82

dimensions of the ellipse

Question 83

the final three define the

Answer 83

position of the orbit relative to the Earth

Question 84

the mean anomaly indicates

Answer 84

the location of the satellite along the orbital path.

Question 85

Keplerian orbit

Answer 85

For a satellite in a truly elliptical orbit

Question 86

For a satellite in a truly elliptical orbit (also known as aKeplerian orbit)allthe
elements

Answer 86

remain constant, with the exception of the mean anomaly which changes with the motion of the satellite, and so increases with time.

Question 87

Satellite Tracking

Answer 87

Knowing the position of the satellite in orbit

Question 88

navigation

Answer 88

• In addition to knowing where a satellite is in its orbit, it is necessary to know the Earth coordinates (latitude, longitude) of the particular scene it is viewing and calculating the Earth coordinates is known as thenavigation.
• Navigation– Calculating the location (latitude and longitude) of the spot being sensed by the satellite.